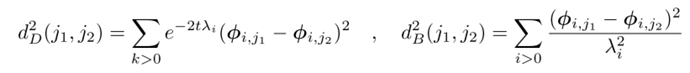本周工作进展
- 项目进展:花了2天时间推进了一下前端,花了一天时间支持俊宇的爬虫展示前端。
- 科研进展:阅读了几篇论文,一篇有关GNN的,还有几篇NAS的,但NAS论文涉及到不少剪枝的东西,没太看懂。
论文分享 《Rethinking Graph Transformers with Spectral Attention》
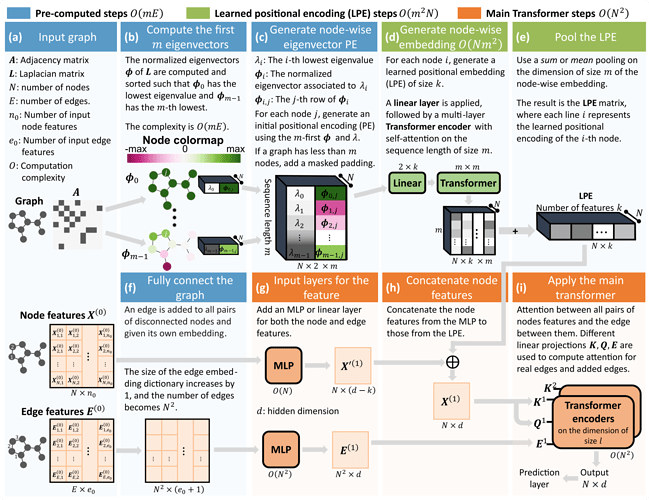
这篇论文主要讲解了如何利用 Transformer 处理图数据。
动机
- 利用 Transformer 的全连接的性质,直接沟通两个节点的信息,避免了 over-squashing 的问题。
- 打破了受限于消息传递机制的表达能力的上限,理论上在区分同构图的能力上变得更强大了。
论文同样点出了基于消息传递机制的范式限制了图的结构,使其不够灵活;作者由此联想到RNN编码序列结构难以解决长时依赖的问题;自然而然的想到了 Transformer 的方法来解决。通过引入 Transformer 可以将通过软归纳偏置编码结构信息,例如位置编码。
贡献
- 该论文的首要贡献就是根植于谱图理论,发展了一套可学习的位置编码方案。
理论动机
Laplace 位置编码功能
-
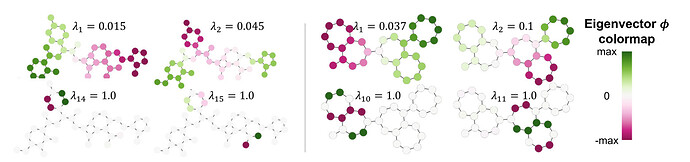
特征向量等价于图上的正弦函数
作者认为在欧式空间里拉普拉斯操作对应于梯度散度,并且他的特征函数对应于正/余弦函数,频率的平方对应于特征值。 -
特征向量能告诉我们两点之间的相对位置信息
-
能从中听到图的子结构
一个合适的 Laplace 位置编码应该重视的东西
-
标准化
对于一个给定的特征值,它的特征空间或许 > 1,为了利用这个信息,必须选择一个特征向量。这里,他采用了L2标准化使得特征向量的模长等于1。 -
特征值
一个排序的特征向量基于他们的特征值的序列,因为频率是预先确定的。然而,这种假设在图中并不适用,因为它们的谱中的特征值可以变化。 -
多重性
当特征值重复的时候,对应多个特征向量经线性组合之后仍是特征向量,这进一步复杂化了为算法计算选择特征向量的问题,并强调了拥有一个能够处理这种歧义的模型的重要性。 -
特征向量数量变化
-
符号不变性
当选中了 k 个特征向量时,有2^k种符号组合情况。 随机翻转。
作者提出的这个位置编码学习模型,直接解决了上述4个问题。